Soeben kam es über den Ticker. Die umstrittene Klausur für den Grundkurs Mathematik der diesjährigen Abiturientia wird nicht wiederholt.
NRW-Bildungsministerin Löhrmann sieht keinen Grund für eine Wiederholung oder ein Noten-Upgrade. Die Hoffnung stirbt zwar zuletzt, aber wir hatten es nicht anders erwartet. Warum auch? Schon die gestrige Abwesenheit der Ministerin, als wütende Schüler vor ihrem Ministerium demonstrierten und ihre später nachgeschobene schmallippige Erklärung, man werde die Argumente der Schüler prüfen lassen, ließen nichts anderes erahnen. Passt ja. Es ging ja nur um ein paar Chancen für so manchen, einen Numerus Clausus zu schaffen, es ging ja – zugespitzt formuliert – nur um die Zukunft unserer Kinder.
Keine Erleichterung für den Jahrgang 2013 – im Gegenteil
Von vorne. Die schriftlichen Klausuren im Abi Doppeljahrgang 2013 sind absolviert. Ich war ja klammheimlich immer davon ausgegangen, dass der Jahrgang 2013 „geschont“ wird und man es ihnen leichter machen würde als den Jahrgängen davor. Schließlich ist es das erste Jahr, in dem auch Schüler nach nur 8 Jahren Gymnasium (G8) zur Reifeprüfung antreten und die Politik mit einem guten Notendurchschnitt beweisen könnte, dass G8 leichterdings machbar ist. Damit habe ich weit gefehlt. Sehr weit gefehlt. Gut, dass ich diese irrige Annahme vorher schön für mich behalten habe. Denn leichter ist hier gar nichts in diesem Jahr.
Vorherrschender Tenor in der mir bekannten Schülerschaft vom ersten Tag an: Die Klausuren sind schwerer als in den letzten Jahren, schwerer und umfangreicher. Zugegeben, jeder Jahrgang empfindet subjektiv seine Prüfungen als „die schwersten von allen je dagewesenen und allen, die noch kommen werden“. Zur umfangreicheren Aufgabenstellung lässt sich natürlich auch sagen: Umgekehrt wird ein Schuh daraus. Wenn eine Aufgabenstellung umfangreich und dezidiert ist, läuft man nicht so schnell Gefahr, in eine falsche Richtung abzudriften. Lassen wir dieses allgemeine Gefühl also unkommentiert.
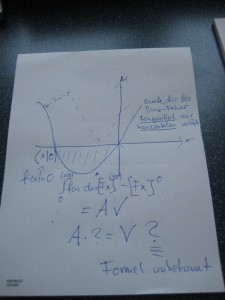
Tangential zur Horizontalen verlaufende Gerade in der Rampe des BMX-Fahrers
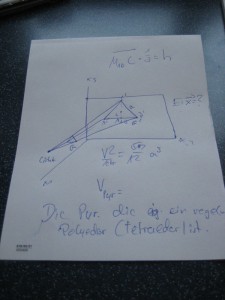
Dann gab es ja noch die umstrittene Mathematik-Klausur. Mein Sohn und einige seiner Freunde haben diese auch geschrieben. Ihr Gefühl ist – vorsichtig ausgedrückt – mies. Die Pyramide, die eigentlich ein regelmäßiger Polyeder/Tetraeder ist, gab ihnen etliche Rätsel auf. Vor allem die Ebene mit drei Unbekannten, deren Fläche ausgerechnet werden musste. Keiner aus dem Grundkurs hat das gekonnt. Die Schüler des Leistungskurses allerdings schon. Bei denen kam das aber nicht dran. Noch schlimmer war die tangential zur Horizontalen verlaufende Gerade in der Rampe des BMX-Fahrers. Ausgebaggert werden sollte auch noch was an dieser Rampe. Dumm nur, dass das keiner berechnen konnte, weil die Formel fehlte. Und selbst wenn man vorher diese Formel hätte lernen wollen, im Tafelwerk Mathematik hätte man sie auch nicht gefunden. Die Formel bei dieser Zeitvorgabe selbst zu entwickeln hätte im übrigen auch die Leistungskurs-Schüler überfordert.
Die Mathe-Klausur strotzte nur so von Spezialfällen, so hatte es das in den vergangenen Jahren in der Tat noch nie gegeben. Vom Oktaeder des Grauens 2008 mal abgesehen. Zudem war die Klausur in der vorgegebenen Zeit nicht zu schaffen. Mein Sohn hat eine Aufgabe, für die es 18 von 100 Punkte gab, für sich selbst zurückgestellt und hatte am Schluß noch max. 5 Minuten Zeit, diese in Angriff zu nehmen. Viele andere Schüler haben eine Aufgabe, für die es 50 von 100 Punkten gab, nicht. Und soweit reicht das Rechenvermögen auf jeden Fall, um zu wissen, bei welcher Note man damit gelandet ist. Mein Sohn hat mir erklärt: Für jede Klausur gibt es drei Gebiete, die egal in welchem Fach, berücksichtigt werden müssen. 1. Re-Organsisation: die Wiedergabe des Gelernten. 2. Transfer: Übertragung des Gelernten auf gestellte Aufgaben. 3. Eigenständiges Denken: in Mathe z.B. die Entwicklung von Formeln, die nicht gegeben sind. Für Punkt 3 hat die Zeit einfach nicht gereicht.
Die Wut richtet sich nicht gegen die Lehrer
Mich macht das Ganze auf der einen Seite traurig, aber auch noch wütender als ich vorher schon war. Ich kann auch rechnen und ich weiß, wenn nicht wenigstens eine 1 vor dem Komma steht, dann war es das mit dem Studienplatz. Ich erinnere an die Benchmark: 1,2 für Germanistik in Bochum in diesem Jahr. Die Wut der Schüler. die sich in sozialen Netzwerken und bei der gestrigen Demonstration entlud, ist berechtigt und verständlich. Die Wut richtet sich übrigens in keiner Weise gegen die Lehrer. Dort ist die Meinung einhellig: Die Lehrer haben in den vergangenen Jahren viel Einsatz gezeigt und getan, was sie konnten, um das eigentlich Unmögliche zu ermöglichen. Wir haben nachgezählt: Wenn man für alle Spezialfälle, die der Lehrplan vorsieht, auch nur eine einzige Stunde veranschlagen würde, wäre man gerade so damit durchgekommen. In G9 wohlgemerkt. Moderne pädagogische Gesichtspunkte wie „Inhalte selbst erarbeiten“ hätte man da allerdings nicht berücksichtigen können, mit der Brachialmethode „Nicht verstehen, einfach lernen“ wäre es vielleicht gegangen.
Von der Bildungspolitik im Stich gelassen
Mittlerweile dürfte auch dem letzten der diesjährigen Abiturienten klargeworden sein, dass sie der im Stich gelassene Jahrgang sind. Jahrelang hat man hier fahrlässig zusammengezimmerte Experimente auf dem Rücken unserer Kinder gefahren, nun sieht man das dicke Ende in Form von überfüllten Unis nahen. Und als Konsequenz stellt man Aufgaben, die kaum lösbar sind, um damit zu „sieben“ und den Notenschnitt möglichst zu drücken? Echt gute Idee. Unglaublich motivierend. So löst man das Bildungsproblem. Bundesländer dieser Nation, schaut auf NRW. Das Bundesland der einfachen Lösungen. Wenn auch nicht in Mathe.
Wir schauen jetzt nach vorne, hoffen das Beste und wünschen dem BVB heute abend mehr Glück, als es unsere Abiturienten mit der Mathe-Klausur hatten…
(Die von mir abfotografierten Skizzen zu den Aufgaben hat mein Sohn nach der Klausur aus dem Gedächtnis gezeichnet, um mir zu erklären, was so schwierig war. Ich habe überhaupt nichts verstanden, das gebe ich ehrlich zu. Fragen dazu kann ich nicht beantworten, aber gerne an den Schöpfer der Skizze weiterleiten.)



Liebe Frau Haase,
ich danke für Ihren Zuspruch. Sie haben Recht: Souveränität ist ein zu Unrecht unterschätztes Talent.
Auch Ihnen nur das Beste und viele Grüsse vonne Emscher !
Liebe Frau Langhoff,
ich finde es mutig, diesen Schritt nach draußen zu wagen, und wir Beide wissen, was es heißt, mit Ahnungslosigkeit zu glänzen. Das Zauberwort in diesem Fall heißt wohl Vertrauen, und dieses lässt sich mathematisch nicht berechnen und beweisen, sondern nur in Ausübung, wenn man es in diesem Fall so ausdrücken kann. Respekt insofern an dieser Stelle an Sie!
Ich habe sachlich-inhaltlich mal überhaupt gar nichts verstanden und bin froh, dass ich mal wieder erlebe, wie sinnlos so mancher Lehrstoff (eher Leerstoff) war, und wie sehr ich mit Wissen, dass ich mir anzueignen hatte, gequält wurde.
Guten Weg weiterhin und Gruß aus Rhein-Main!
Sehr geehrter Herr Grips,
danke für diesen Ihren ausführlichen Kommentar.
Ich schließe daraus, dass Sie eine Klausur im Leistungskurs Mathematik geschrieben haben.
Wie im obigen Artikel eingangs beschrieben, handelt es sich bei der strittigen Klausur um eine Klausur im
Grundkurs, also 3. Abiturfach. Die Zeitvorgabe für eine solche Klausur beträgt 3:00 Stunden. Die Schüler hatten also 3:00 h Zeit für die beiden beschriebenen Aufgaben zuzüglich einer dritten Aufgabe. Hätten die Schüler wenigstens die 3:40 h gehabt, die Sie für die Lösung der beiden beschriebenen Aufgaben benötigten – ich bin sicher, die Empörung wäre geringer.
Das Selbstvertrauen, mit dem sie diesen Artikel schreiben, finde ich, ehrlich gesagt, ziemlich bewundernswert. Sie geben selber, an, von der Materie, in der sich ihr „Sohn und einige seiner Freunde“ mehr oder scheinbar eher weniger erfolgreich bewegen, so gar keine Ahnung zu haben. Sie verlassen sich bei der Beurteilung der Situation also vollkommen auf ihren Sohn, also auf jemanden, der selber, einen, sagen wir, beschränkten Blick auf die Welt der Schulmathematik hat. Dies bewegt sie zu Aussagen wie „Die Mathe-Klausur strotzte nur so von Spezialfällen, so hatte es das in den vergangenen Jahren in der Tat noch nie gegeben“, welche bei genauerem Blick in die Aufgabenstellung eher ungerechtfertigt sind.
Ich hatte selbst die Ehre, mich mit den Aufgaben, die ihr Sohn skizziert hat, 4h 15min auseinanderzusetzen, muss aber gestehen, dass es mir bereits nach 3h 40min gereicht hat und ich, nach ausführlicher Kontrolle, mit einem sehr guten Gefühl abgegeben habe. Vielleicht machen sie sich einfach mal kurz Gedanken darüber, ob vielleicht doch ihr Sohn selber zumindest eine große Mitverantwortung an seinem Scheitern trägt und aus der Mathe-Klausur eine wichtige Lehre mit in seine Zukunft (speziell in ein mögliches Studium) nehmen sollte: Die Hauptverantwortung für den Erfolg in jeglicher Form einer Prüfung liegt in aller erster Linie bei niemandem sonst als ihm selber.
PS: Die von ihnen angesprochene „unbekannte“ Formel steht sehr wohl in jeder Formelsammlung, bei genauer Betrachtung handelte es sich bei dem gesuchten Erdstück nämlich um ein Prisma mit dem Integral als Grundfläche und der gegebenen Breite als Höhe, und die Formel VPrisma lautet (logischerweise): G*h.
Die große „Ebene mit drei Unbekannten“ ergab sich aus dem Gleichsetzen der beiden Abstände von R(x,y,z) zu S bzw. zu T (wie kleinschrittig in der Aufgabe vorher erläutert). Dann dreimal umformen, und fertig.